|
| 2c = 2ae, the distance between the foci of the hyperbola, must equal the field radius plus the oculus radius. |
When the parameters a, b, c and e
are given their usual meanings, the equation of a hyperbola is:
x*x/a*a - y*y/b*b = 1
with
c = a*e
e = c/a
and
a*a + b*b = c*c .
(At a given c, the closer the vertex lies to the center, the more eccentric the hyperbola. An infinitely eccentric hyperbola is a straight line through the center.)
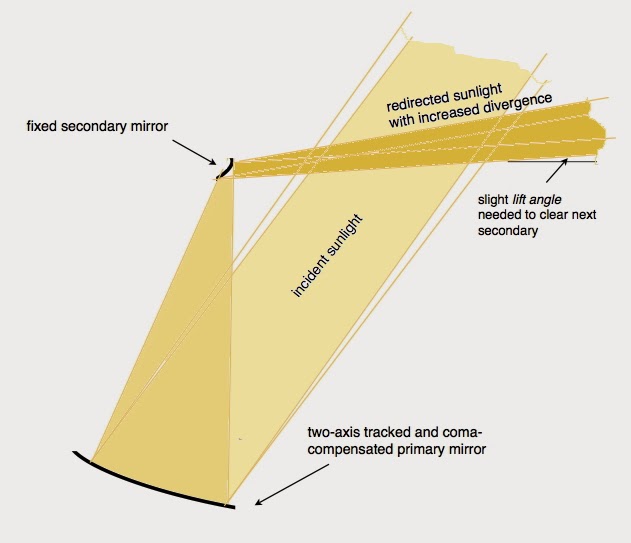
In designing a spindle hyperboloid lens for Veselago beam-down optics, the parameter that must be fixed at the outset is the distance, D, that separates the two foci,
D = 2c = heliostat field radius + oculus radius.
Once we fix c at c = D/2, variation in the eccentricity of the hyperbola varies the radius of the lamp.
The offset, R, of the rotational axis from the center of the hyperbola is
R = c - oculus radius .
Given an offset R, the quartic equation for a spindle hyperboloid can be derived as follows:
 |
| Derivation of the quartic equation for a spindle hyperboloid. |
In a POV-Ray scene description a spindle hyperboloid Veselago lens becomes something like:
#declare a = 1.0; //distance from hyperbola center to vertex
#declare b = 1.0; //asymptote of hyperbola slope = b/a
#declare a2 = a*a;
#declare b2= b*b;
#declare ab2 = a2/b2;
#declare R = 1.8; // offset of hyperboloid rotational axis
#declare R2 = R*R;
….
quartic {
// x^4 x^3y x^3z x^3 x^2y^2
< 1, 0, 0, 0, -2*ab2,
// x^2yz x^2y x^2z^2 x^2z x^2
0, 0, 2, 0, 2*R2-2*a2-4*R2,
// xy^3 xy^2z xy^2 xyz^2 xyz
0, 0, 0, 0, 0,
// xy xz^3 xz^2 xz x
0, 0, 0, 0, 0,
// y^4 y^3z y^3 y^2z^2 y^2z
ab2*ab2, 0, 0, -2*ab2, 0,
// y^2 yz^3 yz^2 yz y
2*a2*ab2-2*R2*ab2, 0, 0, 0, 0
// z^4 z^3 z^2 z Const
1, 0, 2*R2-2*a2-4*R2, 0, R2*R2-2*R2*a2+a2*a2 >
clipped_by
{sphere {<0,0,0>1.0 }}
bounded_by{clipped_by}
sturm
pigment {Clear}
interior { ior -1.0 }
scale <100.0,100.0, 100.0>
translate<0,0,0>
}