Higher frequency (φ + n) phyllotaxis patterns

A phyllotaxis pattern for φ + 20.

Phyllotaxis patterns are often described that have a frequency (i.e., number of dots per turn of the spiral) that is either phi (φ) or phi squared—which is identically phi + 1—but a frequency that is φ plus a larger integer will also work in certain cases. In the plot above, the frequency is phi + 20 dots per turn. A central zone of the pattern does not form a circle packing, but this zone would not be needed in a heliostat array since the central optics would be located there. 

A processing sketch was used to generate these patterns.

Circles packed along a φ + 10 phyllotaxis spiral.

Circles packed along a φ + 20 phyllotaxis spiral.

Circles packed along a φ + 50 phyllotaxis spiral.

These patterns also work with radially oriented ellipses:

36:1 ellipses packed along a φ + 10 phyllotaxis spiral.

36:1 ellipses packed along a φ + 20 phyllotaxis spiral.

36:1 ellipses packed along a φ + 50 phyllotaxis spiral.

Toric curvature of an adaptive primary

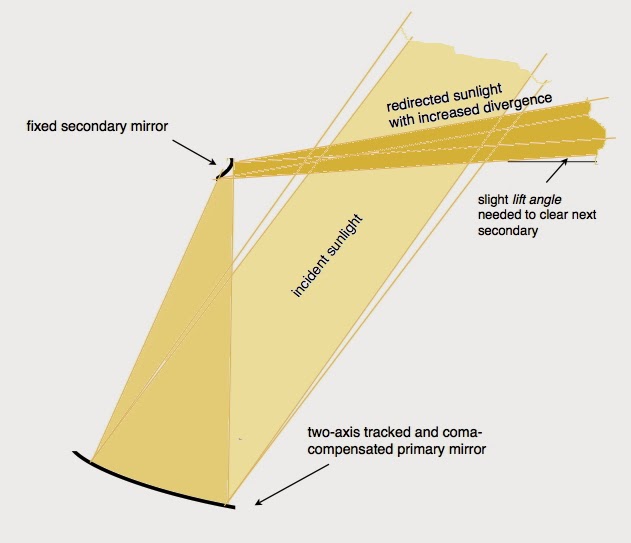
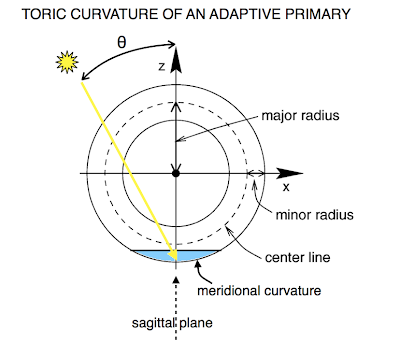
Bending a thin-shell, initially spherical, primary mirror to accommodate the changing angle of solar incidence, θ,  induces a toric curvature in the mirror.

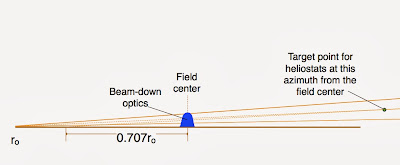
The primary mirror of a two-mirror heliostat must function over a wide range of the solar incidence angle θ: from θ ≈ 0° at summer noon, to θ ≈ 45° at sunrise and sunset. A unchanging mirror profile cannot handle this wide range of incidence angle. It is necessary for the primary mirror to change shape only slightly. Luckily, simple thin-shell bending gives the correct range of profiles.

In the thin-shell bending of a surface, its Gaussian curvature—the product of the curvatures in the two principal planes (the planes that reveal respectively the maximum and minimum curvatures)—is constant. In a spherical mirror these to curvatures are equal, so as a thin-shell spherical mirror bends, one principal curvature increases while the other decreases in the inverse proportion.

Consider a spherical mirror reflecting sunlight. The plane that contains both the sun and the surface normal at the center of the mirror is called the meridional plane. The plane that likewise contains the surface normal at the center of the mirror, but is disposed perpendicular to the meridional plane is called the sagittal plane. When the primary mirror is adapted correctly to the changing angle of solar incidence, the meridional and sagittal planes are also the principal planes of curvature. In particular, as the angle of solar incidence, θ, increases, the radius of curvature in the meridional plane must increase as 1/cosθ, while the radius of curvature in the sagittal plane will, correspondingly, decrease as cosθ.

In the open-source ray-tracing program POV-Ray, a torus is specified by its major radius and its minor radius (as identified in the illustration above.) Thus, in this system, a sphere of radius 1 is also a torus with major radius 0, and minor radius 1.

For correct adaptation to a changing angle of solar incidence θ, we need the meridional radius of curvature (which is equal to the major toric radius plus the minor toric radius) to be proportional to 1/cosθ; and therefore, under the constraint of thin-shell bending, the sagittal radius of curvature (which is equal to the minor toric radius) will be proportional to cosθ.

The Solar Highbeams Project: draft front page for Github

THE SOLAR HIGHBEAMS PROJECT

is an open hardware/software project to improve awareness and modeling of solar furnace power, and develop under creative commons license the required new hardware components. Since developing the hardware components, like those needed for a moonshot, makes no sense without an understanding of how they all will work together, a high priority is developing 3d models and ray-traced images and animations of systems and components that convey the motivation for the work. Needs of the Solar Highbeams Project range from mechanical and optical design, to system optimization, environmental impacts and promotional media.

WHY SOLAR FURNACES?

Renewable energy is often criticized for requiring expensive energy storage, but in a gigawatt-scale solar furnace, storing energy as high-temperature heat is easy, comparatively safe, and, in fact, almost unavoidable. Unique among all sources of power, a solar furnace is primarily a means of making things. In particular, if a solar furnace is itself made mostly of glass, it can make most of the parts for the next solar furnace from inexpensive local raw materials. In so far as solar energy for making glass will be the limiting factor, it appears the doubling time to make parts for the next solar furnace will be only a matter of months. An advantage solar furnaces enjoy over other sorts of solar power is that the solar energy collected travels the last couple of kilometers to the power network, not through expensive copper wires or steel pipes, but as an optical beam, just as freely as it travelled the first 150 million km from the sun to the earth.

WHY TWO-MIRROR HELIOSTATS?

Solar furnaces built to date use many flat mirrors, called heliostats, to redirect sunlight toward a common focus. A consequence of using a single mirror reflection to accomplish the entire redirection of sunlight toward the focus is that the heliostats tend to block each others' view of the focus. That results in both an expansive use of land (the deployed mirror area might be as little as 18% of the land area), and a focus that is uneccessarily high above ground level (typically about 1/7 the radius of the field.) A rough way to put it is that designing a conventional heliostat field is as difficult as designing a theater for Sponge Bob Squarepants  with eyes at the level of his torso. Using two mirrors per heliostat—a large primary mirror near the ground (think of it as the body,) and small secondary mirror mounted high above it (think of it as the head)—permits a heliostat field that uses ground as efficiently as a Broadway theater. Also, the mechanical motions in a field of one-mirror heliostats are all different; with two-mirror heiostats the motions are all the same.

A baseline telescopic heliostat array and its fill and blocking factors

In this baseline design, heliostats at 0.707 r_o operate at their designed beaming angle. The distance (shown out of scale in the diagram) between the field center and the target point is 0.84 r_o.

Previous posts suggested aiming heliostats at a point 0.84 r_o behind the center of the array, and arranging the heliostats with constant spacing along a phyllotaxis spiral, and operating the heliostats at 0.707 r_o at their design beaming angle. We will fix these values as the baseline design.

For a heliostat at a distance r from the center, the distance, d, to the target point is d = r + 0.84 r_o. For the heliostats operating at the designed beaming angle d = (0.707 + 0.84) * r_o = 1.55 r_o. Since all angles are small, the extra elongation of the ellipse for a heliostat at distance r from the center is

(r + 0.84 r_o)/(1.55 r_o) = 0.65 * (r/r_o) + 0.54

Using a processing sketch to apply this elongation factor to each ellipse yields this image:

Secondary ellipses for the baseline telescopic heliostat array. The variable elongation of the ellipses corresponds to a target point at 0.84 ro behind the field center.

Histogram analysis shows:

BASELINE TELESCOPIC HELIOSTAT FIELD PROPERTIES

Land fill factor = 70%
View fill factor = 61%
Secondary blocking factor = 1.4%
                                                       

Targeting and spacing of telescopic heliostats

Summarizing the results of a previous post: in an optimized heliostat field, the farther out heliostats (i.e., beyond 0.707 r_o) should be spaced extra distance apart to accommodate lower aiming angles and the correspondingly increased area of their more elongated ellipses; nearer in, the heliostats should be placed as close as mechanically possible because higher beaming angles will produce less elongated ellipses having less area. (Note that all of the ellipses have the same minor axis dimension—the width of the secondary.)

In the design proposed in that earlier post, the elongation at the last row is 1.50x when the projection is taken for the lowest rays (1.19x when the projection is taken for the central rays.) Even if the heliostat spacing is kept constant, secondary blocking is not too severe. Here are histogram results for 12,000 heliostats arrayed on a phyllotaxis spiral, Baumgardner factor = 0.86, without any extra heliostat spacing.

SECONDARY BLOCKING WITH LOW AIMING

Elongation factor              View fill factor            Blocking factor
1.5                                     85.8%                         10.2%
1.25                                   76.6%                           3.9%
1.0                                     63.9%                           0.8%
0.75                                   48.7%                           0.1%

It seems extra spacing of the outer heliostats is a matter for a more fine-grained optimization to consider. A reasonable baseline design can use target point aiming with constant heliostat spacing.

Quantitative results of packing 12,000 telescopic heliostats along a phyllotaxis spiral

12,000 circles packed by phyllotaxis using Bumgardner factor = 0.86. Land utilization is 0.701.

12,000 ellipses (36:1 aspect ratio) packed on a phyllotaxis spiral with Baumgardner factor = 0.86. The view fill factor is 0.639; the blocking factor, 0.008, is less than one percent. (Multiple overlaps, as occur in the center, are neglected in calculating the blocking.)

Here are some results from generating high-resolution off-screen images in Processing and using a histogram analysis sketch to measure land fill, view fill, and blocking factors when telescopic heliostats are arranged along a phyllotaxis spiral.



PRIMARIES
Bumgardner factor            Land fill factor             Blocking factor

0.92                                  79.5%                           1.6%
0.89                                  75.4%                            0.6%
0.87                                  72.4%                            0.2%
0.86                                  70.1%                              0%              



SECONDARIES
Bumgardner factor             View fill factor              Blocking factor

0.86                                    63.9%                           0.8%

Bumgardner's "fudge" factor is the ratio of the radius of a heliostat to the radius of the imaginary circle encompassing the heliostats share of the field area. With zero blocking, as there is for circles when fudge = 0.86, the land fill factor should be fudge * fudge = 0.74. The difference between 0.74 and the measured 0.70 is the extra field area added beyond the center of the farthest heliostat so that the whole heliostat lies within the field. The importance of this extra margin diminishes as the number of heliostats increases. In a very numerous array, we may take 0.74 as the land fill factor.

It may look like there are a great many heliostats in the images above, but in a GW-scale heliostat field, this many heliostats and more would be displaced by the central optics! Even placing this many heliostats along a phyllotaxis spiral requires a value for the golden angle more accurate than Processing's single-precision functions can calculate.

Phyllotaxis-based packing of secondaries and primaries

A phyllotaxis-based radial packing of ellipses.

This figure, generated in Processing, shows the packing of ellipses with 36:1 aspect ratio. In an arrangement of secondaries the white areas would represent loss of brightness, the darker gray areas would represent blocking loss. Processing source code, based on a program by Jim Bumgardner, is here.

A center-coordinated packing of circles and ellipses. Both the primaries and secondaries of telescopic heliostats can be efficiently packed along the same phyllotaxis spiral.

Several thousand center-coordinated circles and ellipses arrayed along the same phyllotaxis spiral.

Application of phyllotaxis patterns to arrangements of conventional heliostats is described by Noone, Torrilhon and Mitsos in "Heliostat Field Optimization: A New Computationally Efficient Model and Biomimetic Layout."

6000 centroid-coordinated circles and 36:1 ellipses arranged along a phyllotaxis spiral.

The ellipses in these diagrams represent the secondary mirrors projected onto the plane of their center (a physically cast shadow on that plane would only be half an ellipse.) The fact that all the ellipses have the same aspect ratio in these examples means that the secondaries are targeted to a constant beaming angle, not aimed toward a single target point, which would result in more elongated ellipses in the periphery of the field.

When two adjacent ellipses overlap, it means that only one of them is visible from their target: in other words, there is blocking loss. When white can be seen between two ellipses, it means there is a loss of radiance at the focus relative to an ideal concentrator, and therefore a loss of thermodynamic efficiency relative to the ideal.

The flexing of an adaptive primary

The flexing required of an adaptive primary is slight. Though the primary in this video is going through its entire range of adaptation (from 0° solar zenith distance to 90° solar zenith distance) its bending is barely visible. POV-Ray source code here.

Adaptive primary: the movie

This is a POV-Ray ray-trace of an adaptive primary mirror for a telescopic heliostat. (Scene description file here.) The ray tracing was done in Mega POV on a MacBook, the movie frames were put together in Graphic Converter, sound was added with Audacity and iMovie, uploaded to Vine with Vinyet. [mini cooper model ccby gilles tran; music by longzijun]

The thin-shell mirror bends to adapt to different angles of solar elevation. For a sun near zenith, the mirror curvature is nearly spherical, the curvature becomes more toric as the sun sets. Physical bending is not simulated in the program, rather the ideal off-axis parabola is selected for each solar elevation angle. The primary shown is about 3.1 m in diameter.

Why does the photographer's image get reversed left-and-right but not up-and-down? When the mirror is adapted to a sun at zenith (the nominal condition) it's shape is nearly spherical. Standing just inside the center of curvature of this quasi-spherical mirror, the photographer sees his own reflection magnified and upright and undistorted just as in a shaving mirror. As the mirror adapts to lower sun angles, the lens becomes more toric. In particular, its radius of curvature in the sagittal plane gets shorter while the radius of curvature in the meridional plane gets longer. As the mirror flexes, as it does in the first few frames, the increased curvature in the sagittal plane is easily noticed from this vantage point. Towards the end of the film, when the photographer's reflected image is very distorted, the center of sagittal curvature is passing through his head (!), causing left and right to invert. At that same moment the center of meridional curvature has moved far behind the photographer—leaving no chance that up and down will also invert.

The trading off of sagittal and meridional curvature that occurs when a thin-shell mirror is bent is exactly what is required to maintain a constant distance between the focus and the center of the mirror as the sun moves.

An adaptive primary modeled in MegaPOV

Though positioned horizontally, this primary is adapted to sunlight coming from the foreground at a zenith distance of 75°. Notice that the adaptation makes the rim look a little like a potato chip. Simulated in MegaPOV; the Mini is CC BY Gilles Tran.

The scene description is posted here.