Telescopic heliostats: designing heliostats as if thermodynamics mattered

Sunlight falls to the ground in an array of conventional heliostats—and the central tower is unnecessarily tall—because thermodynamics is ignored in the optical design. Since any optical system could be handling thermal radiation, all optical design is constrained by the Second Law of Thermodynamics.

It's not nice to fool Mother Nature. Redirecting sunlight toward a lower angular elevation is a sneaky way to increase its flux—therefore the Second Law of Thermodynamics demands that the light's divergence increase as well. In plain terms, thermodynamics permits us to make the sun look closer, but not hotter.  A high-performance heliostat must be an optical device that increases the flux and divergence of sunlight while keeping parallel rays parallel, in other words, a telescope.

The twin beams of light emerging from these 7x binoculars focussed at infinity and pointed at the sun are quite collimated, even though the solar flux has been increased about 49 times. Calculations indicate that 6x magnification would be optimal for a telescopic heliostat.

The Cassegrain configuration as it is usually described—a parabolic primary with a hyperbolic secondary—is not actually a telescope until an eyepiece is added. A secondary mirror having instead a parabolic profile would move the focal point to infinity, and thus serve as the eyepiece.

The focal egg

Focal egg for an array of telescopic heliostats with constant beaming angle β, outer radius ro, and inner radius ri = 0.2 * ro.

The egg of the Emperor Penguin is shaped something like a focal egg.

Definition: In solar engineering, a focal egg is an imagined directionally-selective blackbody radiator whose radiative emission would replicate the solar flux distribution at the center of a field of heliostats. 

Definition: In solar engineering, a minimal absorber, is the smallest absorber that can absorb all of the solar flux at the center of a field of heliostats.

It may seem that we have great freedom in where we point the beam of each telescopic heliostat. This is not true if we must use the same optics over the whole array, because the optics will have been optimized for a standard beaming angle (i.e., a particular angular elevation of the central ray of the beam.) Since considerable costs may be incurred in using different optics in different parts of the field, a better strategy is to use the same optics at their designed-for beam elevation over as much of the field as possible, perhaps aiming heliostats in the outer portions of the field slightly low, and heliostats in the inner portions of the field slightly high.

Consider an infinite field of telescopic heliostats, all of them having the same beam spread, σ, and beaming angle, β, where β ≈ σ. (Note that β is the elevation of the central ray, not the lowest ray which was used in an earlier post.) The focal zone in this case is an inverted cone with its apex in the center of the field at the same height as the secondaries. Since β ≈ σ, this focal cone has the property base ≈ altitude, making the angle at the apex of the cone about 2 * arctan(1/2) = 53°.

The smallest absorber (gray) that can intercept all of the radiation from a field of telescopic heliostats is a segment of a cone (apex angle slightly more than 53°) terminated by spherical caps. The focal egg is a directional blackbody radiator that mimics the array's flux distribution near the focus.

A practical heliostat field begins at some inner radius r_i and terminates at some outer radius r_o. To minimize the number of parameters in these calculations, we will arbitrarily assume r_i = 0.2 * r_o.

Since the beaming angle, β, and the beam spread, σ, are the same over the whole field, and also σ ≈ β, any light coming from the secondaries is confined to a passband of elevation angles between 0.5 β and 1.5 β. This passband of elevation angles is a fixed characteristic of the light coming from the array until it encounters the beam-down optics.

Suppose we take a ride up the axis of the focal zone. To keep the calculations simple, β is in radians, and we use the approximation tanβ ≈ β.

At first we see no sunlight, because looking as far up as sunlight from the secondaries could possibly be coming from (0.5 β below the horizon,) we can't see any secondaries.

The first sunlight from secondaries will be visible when we reach a height above the secondary mirrors, h, of

h = r_i * 0.5 β = 0.1 βr_o

We will see full flux—the same flux as from an infinite heliostat array—when secondaries fill our passband, our elevation-limited field of view, at a height of

h = r_i * 1.5 β = 0.3 βr_o

The infinite array model will continue to represent what we see until we begin to see desert beyond the farthest ring of secondaries at

h = 0.5 βr_o

The last sunlight from secondaries will be seen when the farthest secondaries are just too far below us to be seen at the steepest angle of elevation:

h = 1.5 βr_o.

We will try to model the distribution of flux near the focus by the contrivance of a directional blackbody radiator—its absorption and emission limited to the elevation passband mentioned above—whose back radiation would cancel the flux from the heliostats. With a finite heliostat array, the cancellation cannot be perfect because there will be locations, especially near the top of the focal zone, where the passband will not be filled: we will see desert where an infinite array would have heliostats. Viewed from  these locations, the directional blackbody, or focal egg, must have a reduced radius to compensate for the partially filled passband of the light from the heliostats.  The focal egg will therefore be somewhat smaller than the minimal absorber, the smallest body that could intercept all of the light coming from the array.

In the height range where the infinite array model can be applied, 0.3 βr_o < h < 0.5 βr_o, the focal zone is an inverted cone. Below the conical range, h < 0.3 βr_o, the flux falls to zero at 0.1 βr_o. Above the conical range, h > 0.5 βr_o, the flux falls to zero at 1.5 βr_o. As illustrated in the upper drawing, the focal egg can be approximated as a short segment of a cone terminated with ellipsoidal caps. The purpose of low-aiming the outer portion of the heliostat field, and high-aiming  the inner portion, would be to make the ellipsoidal caps more oblate.

If the optics of our system are perfect, the focal egg, with its directionally-limited thermal radiation, will recreate the heliostat array's flux distribution when the egg's temperature is that of the surface of the sun. With the oculus also at the sun's temperature, the beam-down optics will need to sited on the locus of satisfying the thermodynamic constraint that the two radiant fluxes are equal. From anywhere on that locus, the oculus will subtend the same solid angle as the portion of the focal egg seen within the passband. Assuming the size of the heliostat array is a given, the only parameters available to vary are the oculus radius and its z coordinate. Hopefully, some combination of those two parameters gives a locus approximately coincident with one of the family of parabolas satisfying the geometric constraint.

Transflective beam-down optics

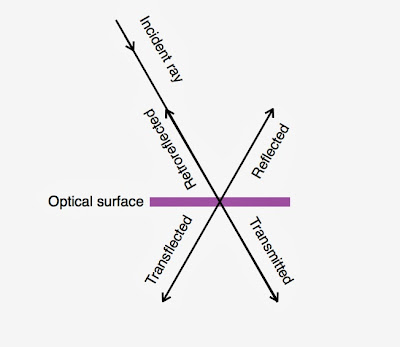Under certain constraints there are only four kinds of optical surfaces: windows, mirrors, retroreflectors, and transflectors.

As mentioned in the previous post, thermodynamics does not require that light arrive and depart from an optical surface at the same angle to the surface normal, but everything is simpler and more efficient in practice if this is the case. A further sensible and practical constraint is that all three vectors (the surface normal, the incident ray, and the emergent ray) all share the same plane. Under those two constraints, there are only four kinds of optical surfaces:

• window: ray emerges on the opposite side of the surface, and in the same direction as the incident ray,
• retroreflector: ray emerges on the same side of the surface, and in the same direction as the incident ray,
• mirror: ray emerges on the same side of the surface, but not in the same direction as the incident ray,
• transflector: ray emerges on the opposite side of the surface, but not in the same direction as the incident ray.

If we know which of these four types of optical surface we are dealing with, the geometry is completely settled, because, under the assumptions, we know both the plane of the emergent ray and the angle it makes with the surface normal.

Windows and retroreflectors, of course, do not form images. Of the two remaining possibilities— transflector or mirror—the former is more practical for solar beam-down optics because a transflector can be mounted directly on the ground rather than atop a tower.

Note that the reflected ray and the transflected ray are always collinear and oppositely directed—so what is a real image for one becomes a virtual image for the other. Imaging transflectors take on the same conic-section profiles as imaging mirrors, but the real-or-virtual property of the image is switched. Beam-down optics for an array of telescopic heliostats must receive light that is propagating nearly horizontally and form a real image at the oculus. Thus the shape we need is the same as that of a mirror that takes horizontal light and forms a virtual image at the oculus. That shape is a surface of revolution whose profile is a parabola having a nearly horizontal axis.

Parabolic curves (representing the geometric constraint on the beam-down optics) superimposed on the back radiation from the oculus (representing the thermodynamic constraint.) Perhaps the outermost of these profiles would operate at a practical level of flux and divergence.

We don't have a lot of freedom in varying the surface determined by the geometrical constraint. We can hope that there is a focal length for the parabola that gives a surface that approximately satisfies the thermodynamic constraint as well. Failure to satisfy the thermodynamic constraint will mean that we either waste light already collected by the heliostat field, or we waste thermodynamic efficiency in converting that collected light to our intended purpose—which really amounts to the same thing.

From the diagram above, it can be seen that the flux on the beam-down optics must increase gradually from zero at the bottom, reach a maximum about halfway up, and then decrease—but flux is still going to be rather high wherever the parabolic profile tops out. At that point the flux must abruptly drop to zero since that light would be overshooting the beam-down optics. The heliostat field—and its targeting—must produce this kind of flux distribution. Even though the flux at the bottom should build up slowly from zero, it will not be economical to operate beam-down at low flux levels. There needs to be a truncation of the optics near the bottom of the parabola as well, and likewise an abrupt drop-off of flux there as well.

Outside these two cutoff angles spherical mirrors are needed to reflect back-radiation toward the oculus. 

Back radiation from the target

Far-field approximation of the radiant flux from a horizontal disk. The region closer than one disk radius from the center of the disk has been blacked out. If the disk is at the temperature of the sun, the remotest black fringe is at 0 suns of flux, the next at 1000 suns, etc.

In a perfect solar concentrator, the target reaches thermal equilibrium (radiative balance) upon reaching the temperature of the sun's surface. Radiant flux is then net zero throughout the system due to the presence of thermal radiation radiated back from the target. In the forward direction, sunlight uniformly illuminates the target; in the reverse direction, back radiation from the target is collimated and beamed toward the sun. When a perfect optical system is in thermodynamic equilibrium, these two fluxes cancel out everywhere.

At any point in empty space, the divergence pattern of the beam of sunlight will be exactly mimicked by the back radiation traveling in the opposite direction. At an optical surface—where light might be redirected and its divergence pattern reshaped—the fluxes on the two sides of the surface must still sum to zero.

Flux on a surface is proportional to cosθ, the cosine of the angle the incident rays make with the surface normal. This is Lambert's Law. The divergence pattern of light at a particular point, P, on a surface can be described as the interior of region drawn on a unit sphere. In geometrical terms, Lambert's Law says that the flux at the surface is not the area of this region on the unit sphere, but rather it is the area of this region after it has been projected orthogonally onto the surface at point P. The orthogonal projection supplies the factor of cosθ.   Our requirement for net zero flux through the optical surface is then that the projected areas for both sides of the optical surface are equal.

There is one part of the optical design we have no control over: the pattern of thermal radiation that will be emitted from the target. In the case of a solar glass-melting furnace, the target is the opening of the furnace, the oculus, which is effectively a horizontal disk. Calculating the flux of back radiation from this disk is merely a problem in visual perspective because it is a perspective view of the disk that determines the shape and area of the region on the unit sphere. According to Lambert's Law, we should follow upon that exercise in visual perspective with an orthogonal projection onto some surface (whose orientation would be somewhat unclear at this point,) but, if we assume the angles of incidence to be the same on both sides of the optical surface (a desirable condition for both efficiency and simplicity,) that step is unnecessary. We will make that assumption.

The problem in visual perspective gets a bit complicated close to the disk, but in a far-field approximation the horizontal disk appears as an ellipse, one angular dimension being proportional to 1/r, and the other to cosθ/r.

More precisely, taking the radius of the oculus = 1, and r = sqrt(x² + y² + z²),

the angular extent of the ellipse in the horizontal (non-foreshortened) dimension = 2 * arctan(1/r), or approximately 2/r,

and the angular extent of the ellipse in the vertical (foreshortened) dimension, is approximately cosθ * 2/r.

Therefore, our perspective view of the disk translates approximately into an elliptical region on the unit sphere having an area, measured in steradians, of cosθ * 4/r² * π/4 = πcosθ/r².

The angular diameter of the sun is .01 radians, so a flux of 1000 suns corresponds to an image of the sun covering 1000 * π * (.005)²  =  .079 steradians.

The graphic above shows the far-field approximation of the thermal flux from the oculus. When the disk is at the sun's blackbody temperature, each fringe represents 1000 suns, that is, the remotest black fringe is at 0 suns, the next black fringe is at 1000 suns, etc. To give a sense of scale, points closer to the center of the disk than one disk radius have been blacked out, but the far-field approximation is not actually good enough to go in that close.

Beam-down optics for telescopic heliostat arrays

The focal zone of an array of telescopic heliostats scaled to 140 m height—yielding about 750 MWe.

Save for the intervention of the beam-down optics, light from a field of telescopic heliostats would converge onto a focal zone shaped something like an ice cream cone (the orange region in the figure above.)

Taking parameters from an earlier post:

Height to top of the beam-down optics: 140 m

Field radius: 1085 x 1.59 = 1725 m

Beam divergence: 3°

Angular elevation of beam center = 1.6° + 1.5° = 3.1°

[For comparison: the height of the Washington Monument is 169 m (152 m to the base of the pyramidal cap); the distance between the monument and the U.S. Capitol is 1800 m. The Capitol's dome is 88 m in height and 29 m in diameter.]

If it received only light from the outermost ring of heliostats, the focal zone would be a sphere centered at 1725 m x tan(3.1°) = 93 m high, with a radius of 1725 m x tan(3°) / 2 = 45 m. That is the "ice cream" at the top of the cone; superimposing many smaller and lower spheres for each ring of heliostats yields the "cone" itself. 

The beam divergence of a 6x telescopic heliostat (the pink spot) drawn as an area on the globe.

The beam divergence found near the center of an array of telescopic heliostats. Divergence has increased in longitude, but not in latitude.

We will describe the directions light propagates in by reference to an earth globe oriented with north pointing up, and with the prime meridian facing the heliostats we are concerned with. So, for example, close to the heliostat, the light lies within a circle 3 degrees in diameter that is centered on 0 degrees longitude and 3.1 degrees S latitude (the top picture above.) Closer to the focal zone, the light will have the same latitudinal extent, but its longitudinal extent will have increased because the light of many heliostats is being concentrated along that dimension (lower picture above.) The exact longitudinal extent can be calculated by taking a look in the opposite direction and calculating the angular subtense of the cone-shaped focal zone.

At times we need to know the divergence of light where the beam-down optics are located. We can get the same answer by reversing the light rays and considering the focal zone—rather than the heliostats—as the source of light.

Some considerations in designing beam-down optics:

1. Placing beam-down optics too close to the focal cone will make the incident light too widely spread out in the longitudinal direction to be handled efficiently by the optics.
2. We want the surface normal of the beam-down structure to make roughly equal angles with the incoming and outgoing light. This will avoid the same thermodynamic "gotcha" that afflicts conventional heliostat fields that direct high sun to a low target. 
3. We want the incident light to cover the same area on the globe (i.e., subtend the same solid angle) as the opening of the furnace, because that is what we can do most efficiently, reshape, not resize, divergence. 

Un-silvered mirrors

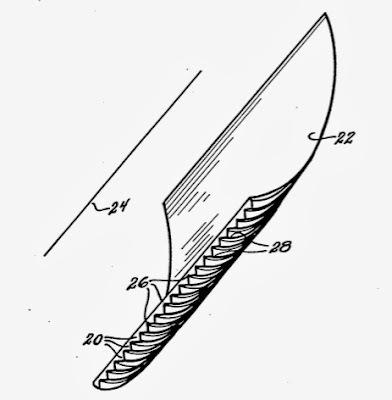A solar concentrator with prismatic reflectors. Rabl & Rabl US4120565.

In making an all-glass solar furnace it would be desirable to avoid the use of silvered or aluminized mirrors. The use of prismatic reflectors, is a possibility for telescopic heliostats. The primary mirror tracks the sun precisely in azimuth, and the secondary mirror sees a stationary light source of only 3° divergence. Both of these situation are ideal for prismatic reflectors...

...on second thought, I don't think this can work. The optics of these surfaces depend on the dihedral line rather than the surface normal. For example, in the image of the trough concentrator above, if the prisms ran in the longitudinal direction there would be no concentration because there would be no curvature of the dihedral lines. This technique seems to need radial symmetry to form an image.

Optimizing telescopic heliostat arrays

Whoops! Looks like most of the sunlight is hitting the ground.

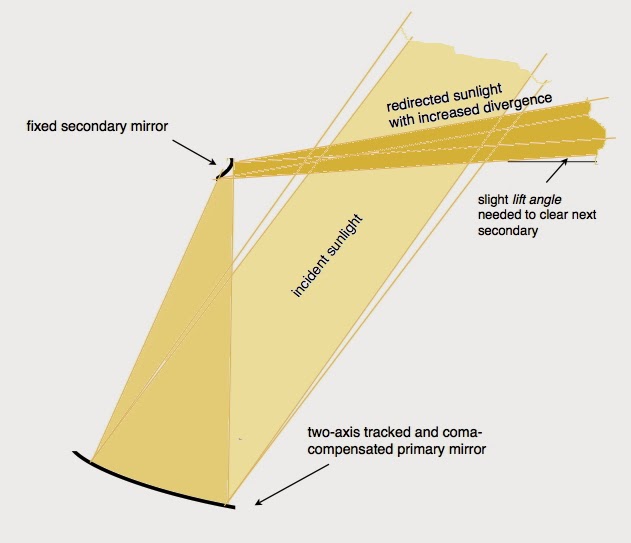
Conventional heliostat arrays have about 33% land utilization—most of the available sunlight strikes the ground! The angular elevation of the top of the tower as viewed from the farthest heliostat is about 7.4 degrees, or a run-over-rise of about 7.8. Telescopic heliostats can do better on both accounts.

Economic optimization of a heliostat array is a Godzilla of a problem requiring full cost data, full knowledge of the operation of the rest of the plant, and full knowledge of the solar resource. A simpler option is available for telescopic heliostats: we can simply design for negligible loss of available sunlight. (This is not an option with conventional heliostats because flat mirrors start blocking each others' view of the target long before they are packed closely enough to collect most of the available light.)

"Designing for negligible loss of available sunlight" in practice means packing the primaries closely and designing the secondaries on the basis of their lowest ray (i.e., the ray most likely to be intercepted by the back of another secondary.)

Closely packed primary mirrors shade about 90% of the land area in the worst case (sun at zenith.) Utilization improves as the sun lowers and the primary mirrors tilt up.

It is also necessary to avoid blocking (redirected light hitting the back of secondaries) if we want to avoid wasting light. We will consider a particular case.

Consider a telescope of linear magnification six. It intensifies sunlight 36 times while increasing its angular divergence by a factor of six. The beam spread of natural sunlight is 0.5°, so the sunlight emerging from the eyepiece of a 6x telescope will have a beam spread of 3°. To accomplish that increase in divergence requires the secondary mirror to be six times closer to the focussed image of the sun than the primary mirror that formed the image. The secondary mirror is tilted about 45° to redirect vertically upward sunlight to nearly horizontal, so it will have an oblong planform, but viewed from directly above (or from the distant central tower), it appears nearly circular, and this circle has one sixth the diameter of the primary mirror.

The now familiar figure below can represent this situation if the ellipses (which as-drawn have 9:1 aspect ratio) are redrawn to a 36:1 aspect ratio while keeping their area the same. Recall that the ellipses in this diagram represent the shadows cast on the ground when the secondaries are illuminated by an imaginary light source located at a design point on the beam-down optics. Since we are interested in minimizing blocking, this design point must be where the lowest rays from the secondaries converge—not their central rays. The 36:1 shadows cast by essentially circular objects are evidence that the imaginary light source is at a run-over-rise of 36:1, or an angular elevation of 1.6°. To this must be added the full 3° beam spread of the light emitted by the secondaries, placing the top of the beam-down optics at an angular elevation of 4.6°, a run-over-rise of 12.4.

Thus, for a given tower height, a telescopic heliostat array has about 1.59 times the radius and 2.5 times the area of a conventional heliostat array. It also has about three times the land utilization, giving overall a plant rating about 7.5 times that of a conventional system.

Primary mirrors can be close packed in a telescopic heliostat array without causing the secondaries to block each other.

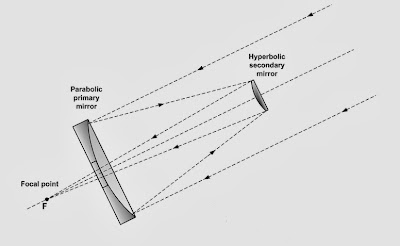
In what sense are telescopic heliostats telescopic?

A pair of binoculars focussed at infinity and aimed at the sun emit intense beams from the eyepieces.

Definition: A telescopic heliostat is a heliostat in which the emergent rays are increased in concentration and divergence.

A telescopic heliostat is not telescopic in the sense that it can throw a beam of sunlight farther. If that were the only consideration, a plane-mirror heliostat would be the best choice. A telescopic heliostat concentrates sunlight while keeping the emergent rays as parallel as possible—which is precisely the action of a telescope focussed at infinity. An inevitable consequence of the concentration, is that the emerging light rays are more divergent than a natural sunbeam, so beam spread from a telescopic heliostat is greater than from a conventional heliostat.

An optical cross-section of a telescopic heliostat shows it to be an afocal, off-axis, Cassegrain telescope. Both mirrors are parabolic.

The object of a heliostat is to hit a target of low angular elevation. (Note how much sunlight falls to the ground in the process.) Image quoted from NRG Energy.

If hitting a distant target were the object of a heliostat we would stick with plane mirrors; but the object of a heliostat is to hit a low target. There are practical limits to the height that a boiler or beam-down optics can be elevated above the ground, so the goal of a heliostat is to redirect sunlight to a target of low angular elevation.

When 100% of the sunlight incident on a horizontal surface at angle of incidence θ_i emerges redirected at an angle of reflection of θ_r, the sunlight has been concentrated by a factor of cosθ_i / cosθ_r . The Second Law of Thermodynamics forbids this concentration without a compensating increase in divergence. Since plane mirrors cannot accomplish the required increase in divergence, they cannot accomplish the desired efficient redirection of light.

Consider, for example, the Ivanpah Solar Project in California. According to the 2010 environmental impact statement for this project, each power tower is 140 m tall measured to the top of the boiler. Ivanpah units 1 and 2 each have 55,000 heliostats, with each heliostat carrying 14 m² of mirror. Let's say 1 m² of mirror typically shades 1.5 m² of ground. Each unit occupies about 915 acres (3.7 million m²) of land, but only 55,000 x 14 x 1.5 = 1.2 million m2 are typically shaded, a land utilization of only a third. To achieve full utilization we would need to squeeze three times as many heliostats into the view above—but they would only block each others' view!

Mutual blocking is worst at the farthest edge of a heliostat field, so land utilization there is really poor. Ultimately it makes more sense to build another tower than to extend a low-utilization field to greater radius. Approximating an Ivanpah unit as a circle, it has a radius of 1085 m. From the farthest edge of the field the top of the boiler has an angular elevation of arctan(140/1085) = 7.4°.

Bending thin-shell primary mirrors to correct off-axis astigmatism

A problem in designing a telescopic heliostat is the need for the primary mirror to image the sun's disk over a wide range of incidence angles. In low latitudes the sun is often directly overhead (90° solar elevation), but useable insolation may still be available down to 15° solar elevation. Assuming the primary mirror is tracked to redirect the incident sunlight vertically, the angle of incidence that the primary mirror of a telescopic heliostat needs to accommodate runs from 0° to a maximum of about 37.5°.

The optical geometry becomes easier to visualize if we forget about tracking and redirecting the sun's light, and simply imagine the primary mirror to be stationary and horizontal while the sun's angle of incidence changes and the focussed image of the sun moves about.

The off-axis astigmatism of a spherical mirror can be corrected by thin-shell bending.

The distance between the mirror and its image of the sun is the focal length, L. The focal length is a function, L(θ), of the angle of incidence, θ. At normal incidence, the focal length of a spherical mirror is half its radius of curvature. Normalizing the mirror's radius of curvature to unity, we have:

L(0) = 1/2

At larger angles of incidence astigmatism appears, that is, sections of the mirror that lie in different planes have different focal lengths. In particular, a narrow strip of mirror lying in the meridional plane (the plane that contains both the incident ray and the mirror normal) will act like a fixed mirror solar concentrator, always bringing sunlight to a focus somewhere along a circle that contains both the mirror and the 0°-incidence focus. In contrast, a narrow strip of mirror lying in the sagittal plane (the plane that contains the incident ray but is perpendicular to the meridional plane) will act like a solar trough concentrator, always bringing sunlight to a focus somewhere along a horizontal line passing through the 0°-incidence focus.

Observing the geometry of a circle in one case, and a line in the other, we have for the meridional focal length, L_m, and the sagittal focal length, L_s:

L_m(θ) = 1/2 * cosθ

L_s(θ) = 1/2 * 1/cosθ

By bending a curved mirror we can tradeoff the two principal curvatures. In the case that the mirror is a thin shell, the product of the two principal curvatures (i.e., the Gaussian curvature,) will remain constant—and thus the product of the two radii of principal curvature will also remain constant. For the radius of curvature in the meridional plane, r_m, and the radius of curvature in the other principal plane (the vertical plane perpendicular to the meridional plane,) r_s, we have:

r_m * r_s = 1

These new radii of curvature simply re-scale the geometric expressions for the loci:


L_s(θ) = r_s/2 * 1/cosθ

L_m(θ) = r_m/2 * cosθ


We would like to bend a thin-shell spherical mirror to make the sagittal and meridional focal lengths equal:

r_s/2 * 1/cosθ = r_m/2 * cosθ

r_s = r_m * cos²θ.

Substituting r_m = 1/r_s,

r_s = 1/r_s * cos²θ

r_s = cosθ.

Substituting this value of r_s into the geometric expression above gives:

L = 1/2.

The focal length of a spherical mirror is independent of the angle of incidence after it has been corrected for astigmatism by thin-shell bending. This is just the result we would wish, as it means the separation between primary and secondary mirrors in a telescopic heliostat can remain fixed.

Optimal packing of telescopic heliostats

Telescopic heliostats can be arrayed such that the sun sees a packed array of primary mirrors and the beam-down optics sees a packed array of secondary mirrors.

Is it possible to arrange telescopic heliostats such that the sun sees a packed array of primary mirrors while the beam-down optics sees a packed array of secondary mirrors?

The figure shows that the answer is yes. (Ironically, it's the same figure as in the previous post, but it is illustrating a different point.) See the the circles in the figure as primary mirrors viewed from the sun's perspective, and the ellipses as shadows cast on the ground by the secondary mirrors when they are illuminated from the direction of the beam-down optics. For example, in the illustrated case, the center of the field can be imagined to lie somewhere far beyond the lower left corner of the image. Extending this arrangement of telescopic heliostats with radial symmetry completes the design for one annular portion of the field. (It is always necessary to segment a heliostat field into annular zones because more heliostats must be incorporated in annular zones of greater radius.)

Because the tracking motions and optics are identical over an array of telescopic heliostats,  the optimum field arrangement of telescopic heliostats always has radial symmetry.

Reshaping divergence with lenslet arrays

Two lenslet arrays, separated by one mutual focal length, can be used to reshape the divergence of a light beam.

Optics near the central focus of a solar plant operates at high energy flux, for example, at the beam-down optics of a glass-making solar furnace the flux will be on the order of 100 suns. This creates both the need to operate at high optical efficiency, and the opportunity to employ more expensive optical solutions than are possible on surfaces of larger area.

Each point on the beam-down optics of a solar furnace will see the circular opening of the furnace (because it is distorted by perspective) as approximately an ellipse. The beam-down optics needs to redirect approximately horizontal radiation coming from the field of telescopic heliostats downward toward the furnace opening. It also needs to reshape the divergence of the radiation to fit inside the approximately elliptical angular extent of the furnace opening.

A simple way to reshape divergence is with two lenslet arrays of the same focal length, separated by one focal length. In effect, each array acts as a field lens for the other. As the figure above illustrates, the lenslets in the two arrays do not have to have the same shape (though they must have the same area) in order to be in perfect correspondence with the lenslets in the other array. For example, in the figure above, circularly divergent light entering through the elliptical lenslets, would exit the round lenslets with elliptical divergence. 

Solar plants don't need us.

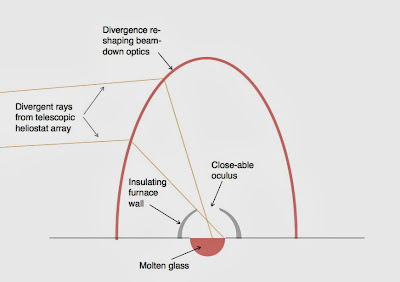Beam-down optics for making glass in a solar furnace using an array of telescopic heliostats.

A common assumption is that the purpose of a solar plant is to produce electricity. That is incorrect. The purpose of a solar plant is to reproduce itself. Electricity is just the reward we symbionts get for helping reproduction along.

The easiest way to make a solar plant that can reproduce itself is to form it out of glass. The raw materials of glass are very cheap, except for one—high-temperature heat—and that is precisely the resource a solar furnace produces in abundance.

Overall view of a glass-making solar furnace employing an array of telescopic heliostats.

An order-of-magnitude calculation of the reproductive rate of an all-glass, solar glass-making plant can be attempted.

Direct normal insolation in Tucson averages just over 7 kw-hr/m2 per day. Assume one-fifth of this flux is collected by the glass-making plant per horizontal square-meter of its total land area, or about 1.4 kw-hr/m2 per day. Assume the total glass used in building such a plant is equivalent to a 2-cm thick layer of glass covering the land area of the plant, or about 50 kg/m2. Assume the thermal energy used in making glass this way is similar to the energy intensity of industrial glass-melting and refining, which is 6.5 MMBtu/ton, or about 2 kw-hr/kg of glass. Thus each square meter of land area needs to produce 2 kw-hr/kg x 50 kg = 100 kw-hr in the time it takes for a plant to make a copy of itself. Under these assumptions, the time required is 100 kw-hr/(1.4 kw-hr/day) = 71 days.

If glass-making is indeed the limiting factor, a single glass solar furnace can spawn a thousand glass solar furnaces in ten reproductive cycles, or about two years. If we don't need such a high rate of growth, we can parasitize the plants with radiant boilers and make some electricity on the side.

The necessity of telescopic heliostats

A telescopic heliostat converts sunlight into an intense—but slightly divergent—beam of light.

A drawback of solar power plants that use mirrors (heliostats) to beam sunlight onto an elevated target is that one heliostat might block a neighboring heliostat's view of the target. Trying to reduce this blocking causes the land utilization of an optimized plant of this type to be low. Since the blocking problem is the worst at the far edges of the heliostat field, for a given target height, the blocking effect also limits the useful radius of the heliostat field—and thus limits the power rating of the entire plant.

The heliostat blocking problem is actually a consequence of the Second Law of Thermodynamics: thermal radiation cannot be concentrated without increasing its divergence. When we try to redirect sunlight from a high-elevation sun toward a low-elevation target using an array of parallel mirrors, we are attempting exactly such an evasion of the Second Law.

Redirecting sunlight toward a low elevation target without a compensating increase in beam divergence is an attempt to evade the Second Law of Thermodynamics—the heliostat blocking effect rises up to trump our attempt.

A telescopic heliostat, by dealing realistically with the need for increased beam divergence can largely eliminate the heliostat blocking problem, and thereby increase by an order of magnitude the power rating of a solar plant having a given target height. About half of this prospective improvement comes from increased utilization of land within the heliostat field, and half from increasing the useable radius of the field. 

Concentrating a sunbeam causes its divergence to increase: that fact is inescapable. Nonetheless, there is room to increase the divergence of natural sunlight. For example, a very narrow-beam flashlight may have a beam divergence (the full angular spread between its half-intensity shoulders) of 5 degrees. That is about ten times the divergence of natural sunlight. So a sunbeam can be concentrated about 100 times without increasing its divergence beyond that of a very narrow-beam flashlight beam.

This narrow-beam flashlight has about ten times the divergence of natural sunlight.  Concentrating a sunbeam to this level of divergence allows a hundred-fold increase in intensity.